I was thinking of "a" as a wheel flip.
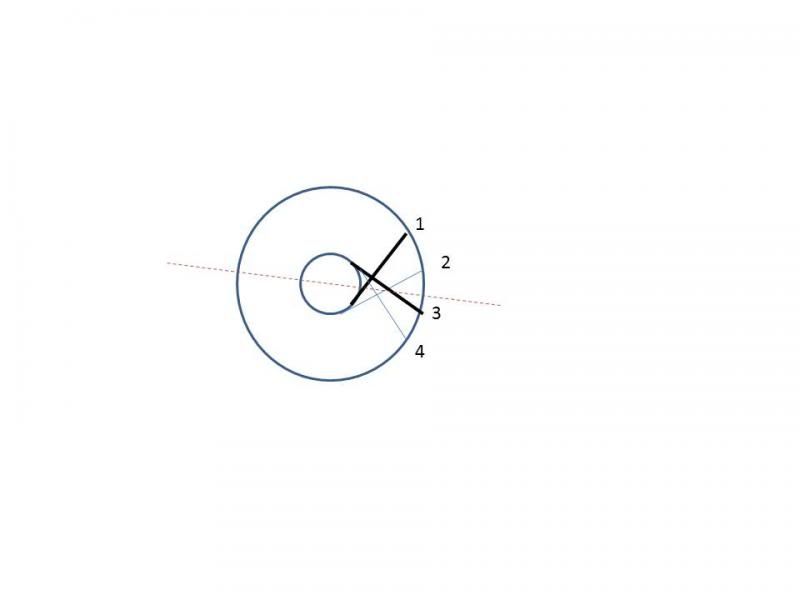
Looking closely at my rear wheel, this is how the spokes look. Spokes 1 and 3 are hooked to the near flange of the hub, 2 and 4 to the far flange. Flipping the wheel around the dashed line will take 1 to where 4 is and 2 to where 3 is... making the picture look just the same, so it is a symmetry. And of course flipping twice is like not flipping at all, i.e. a*a = 1.
b is a rotation, taking one cluster of 4 spokes around to the next cluster of 4 spokes. On a 36 spoke hub, there will be 9 clusters, and rotating through all 9 is a 360 degree rotation, i.e. no rotation at all, so b**9 is 1.
a*b is really a single element of the group - you can multiply elements together any which way, and the result is always just some other element. Of course, some of the elements might get a bit more difficult to think about or describe than others! So in this case, a*b is a flip then rotate. That is still a symmetry operation and a member of the group.
What's curious to me is that a*b seems to be a generator of the group for a 36 spoke wheel... but not for a 32 spoke wheel! If b**8=1, then (a*b)**8 is just 1. There need to be an odd number of 4 spoke clusters for there to be a generator of the group!
All this got me to take a closer look at the spoke pattern on my wheels!